12.0 ACCURACY AND POINT DENSITY SPECIFICATION
12.1 Point cloud accuracy levels
Accuracies can be expressed in 1 dimension – 1D, 2 dimensions – 2D or 3 dimensions – 3D and is discussed in Section 12.4. Often accuracies are expressed in horizontal (2D) and vertical components (1D) because data are generally projected to a horizontal coordinate system (e.g., State Plane), which is separate from the vertical coordinate system and datum (e.g., NAVD88 mean sea level). GNSS uses the ITRF (International Terrestrial Reference Frame) realization of the WGS84 (World Geodetic System 1984) datum, which does not require a projection. Hence, typically MLS data is initially processed in ITRF coordinates, enabling true 3D accuracy assessments. For more details on 3D coordinate systems and geodesy see Hoffman et al. (2006, 2008).
12.1.1 Accuracy specification for MLS
For the purposes of reporting MLS accuracy, two different types of accuracy will be defined: Network Accuracy and Local Accuracy. These types of accuracy are defined by the Federal Geographic Data Committee (FGDC) Geospatial Positioning Accuracy Standards Document # FGDC-STD-007 as:
Local Accuracy – The local accuracy of a control point is a value that represents the uncertainty in the coordinates of the control point relative to the coordinates of other directly connected, adjacent control points at the 95-percent confidence level. The reported local accuracy is an approximate average of the individual local accuracy values between this control point and other observed control points used to establish the coordinates of the control point.
Network Accuracy – The network accuracy of a control point is a value that represents the uncertainty in the coordinates of the control point with respect to the geodetic datum at the 95-percent confidence level. For NSRS network accuracy classification, the datum is considered to be best expressed by the geodetic values at the Continuously Operating Reference Stations (CORS) supported by NGS. By this definition, the local and network accuracy values at CORS sites are considered to be infinitesimal, i.e., to approach zero.
Recommendation: Accuracy values should always be reported following the FGDC standard.
12.1.2 Point cloud density levels
For MLS, point cloud density (resolution) is strongly dependent upon the nominal distance to the target where the point spacing is measured as well as the angle of incidence. For example, if 1,000 points/m2 is obtained on the pavement surface (assuming a scanner height of 2 m above the pavement and a single pass), a much lower point density of 10 points/m2 would be obtained on an adjacent building or cliff surface 20 m away. The statement of work should be clear as to which features are important for the acquisition and what desired point densities should be obtained on those features. Table 1 can be used as a guide for determining appropriate point densities for applications. However, note that it may not be economically feasible or realistic to obtain very high point densities (>points/m2) on objects that are further than 50 m from a navigable path.
To determine the sample spacing (i.e., distance between sample points) from point density values, the following equation can be used:
Values have been pre-computed for select values in Table 8.
Table 8: Point density to sample spacing conversion table.
12.2 Definition of Data COllection Category specifications
The Data Collection Category (DCC) concept for specification of an MLS survey presented in Part I will require the contractor to specify the required network and local accuracy, along with required point density. Because of the varied uses of MLS and the different accuracy requirements of transportation organizations it is impractical to specify finite DCC specifications. Therefore, we recommend the use of a continuous scale. The following notation should be used to specify the accuracy and density of MLS data required for a particular project:
N-????-L-????-D-####
Where N notates the required network accuracy, L the required local accuracy, and D the required point density. The values for “????” should be specified in millimeters, and the value of “####” specified in points/m2 on the target(s) of interest. The specified accuracy will, according to FGDC standards, be specified in 3 dimensions (3D) and quoted at a 95% confidence level. Note that for these specifications, the value of L is always less than or equal to the expected accuracy for N. In other words, local accuracies will always be equal to or better than network accuracies.
12.3 Using DCC specifications
The following three examples are suggested accuracy levels for the three generalized DCC categories of MLS survey type (Table 1). The intent here is to not specify three required levels of accuracy, but rather to give typical or suggested use of the DCC specifications for these three broad categories.
Accuracy Level 1
Typical requirements for a MLS dataset with accuracy level 1 require a 3D network accuracy of 5.0 cm (2”) at 95% confidence level, with a minimum point density of 100 points/m2 (9 points/ft2). This would be expressed in the DCC specification as:
N-0050-L-0050-D-0100
Accuracy Level 2
Typical requirements for a MLS dataset with accuracy level 2 require a 3D network accuracy of 20 cm (7.9”) at 95% confidence level, with a minimum point density of 30 points/m2 (3 points/ft2). This would be expressed in the DCC specification as:
N-0200-L-0200-D-0030
Accuracy Level 3
Typical requirements for a MLS dataset with accuracy level 3 require a 3D network accuracy of 1.0 m (3.28’) at 95% confidence level, 3D relative accuracy of 0.30 m (1’) at 95% confidence level with a minimum point density of 10 points/m2 (1 points/ft2). This would be expressed in the DCC specification as:
N-1000-L-0300-D-0010
12.4 Conversions between accuracy measurements
Often, differences between known control locations and/or control surfaces and the point clouds will be computed as root mean square error (RMSE) values. In order to scale these RMSE values to a 95% confidence level, the following conversions (Hoffman, 2008) should be used, which are based upon the assumption that the errors are Gaussian (or normally distributed):
3D 95% confidence = 3D-RMSE x 1.6166 (4)
Horizontal (2D) 95% confidence = 2D-RMSE x 1.7308 (5)
Vertical (1D) 95% confidence = 1D-RMSE x 1.9600 (6)
12.5 Typical NLD values for applications
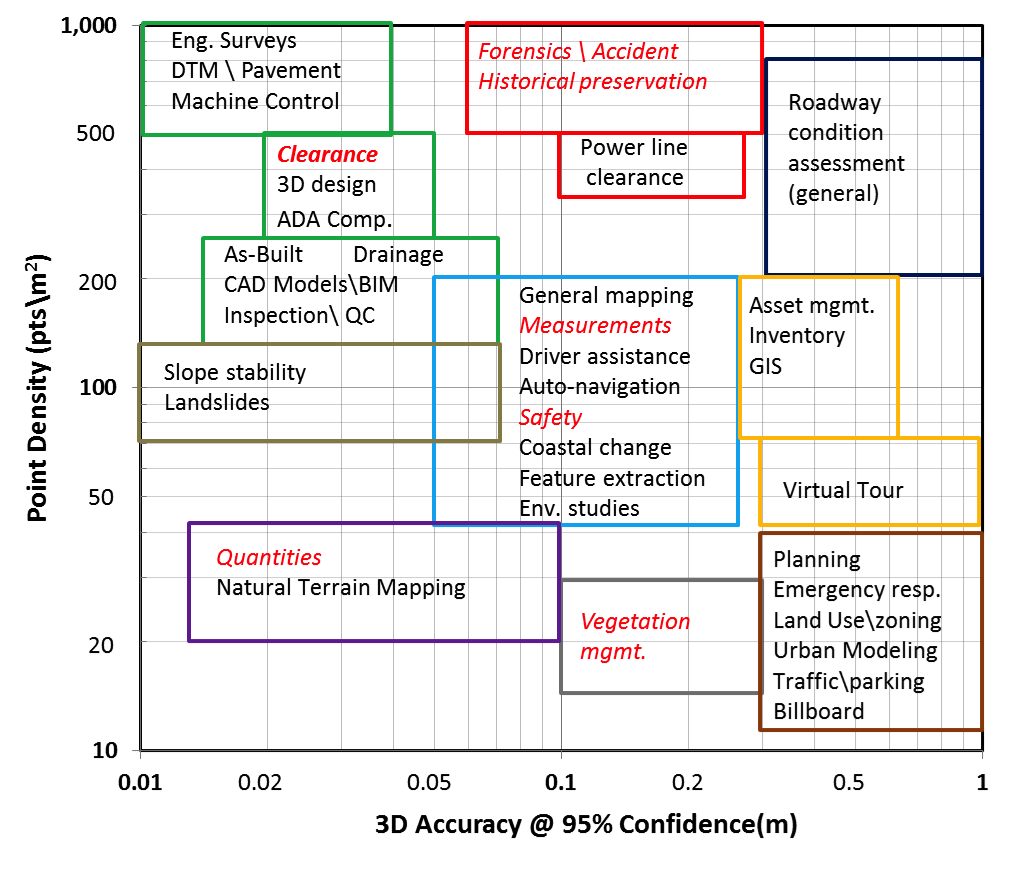
Herein, we provide typical ranges of accuracies (local) and point density values for MLS data common in transportation applications (Figure 10). These have been refined from the general DCC categories defined in Part I. Note that:
- These values are suggested for use as a starting point for a transportation agency. They were determined based on information from the literature review, questionnaire, and project team experience. However, actual project and agency needs may vary.
- The values are meant for data collection to ensure that the data can support the end goals. In some cases, it may be appropriate to deliver a point cloud or model of reduced density for workability. These needs should be communicated clearly in the statement of work.
- These values are for accuracy values expressed at the 95% confidence.
- Accuracy values shown are 3D – not just horizontal and vertical components.
- Point density values are to be evaluated on the targets of interest, which may be up to 75 to 100 m from the vehicle’s trajectory.
- Applications shown in red italics can likely have a more relaxed network accuracy than the relative accuracies shown in the figure.
- When in doubt, specify a higher point density and/or accuracy to be conservative.
It should also be noted that existing COTS design software packages may not be capable of processing extremely large/dense point clouds. In that case the following, alternative workflow can be used for digital terrain modeling. Note that several other viable approaches could be implemented.
- Select a workable tile size and segment the point cloud into these tiles.
- Create a digital terrain model for each tile using all of the ground scan points in that tile.
- Select a desired XY grid size, such as 1 foot by 1 foot, and interpolate the elevation from the DTM at each of the grid intersections within each tile.
- Create a “sampled” DTM from the grid points for each tile.
- Export the sampled DTMs to an engineering design software where they can be combined into a unified DTM for the entire project. If the design software is not capable of combining the tiles then this may have to be done prior to import.
Note that the use of breaklines extracted from the LIDAR data (or other technique) is also encouraged to define key features within the DTM and reduce the number of points required for the model. It may also be possible to use an optimization process that reduces the triangle count in redundant areas while preserving overall DTM accuracy.